Enquanto que medidas da quantidade de inóculo fornecem uma boa avaliação do progresso de epidemias, a observação directa de inóculo nem sempre é praticável ou possível. No entanto, na maioria das doenças de plantas existem sintomas que são observáveis, os quais nos permitem contar o número de plantas infectadas ou estimar a quantidade de tecido infectado. Existe um atrazo entre a ocorrência da infecção e o aparecimento de sintomas visíveis. A manifestação de sintomas pode ser afetada pelas condições ambientais, mas em geral o progresso dos sintomas é paralelo ao progresso da produção de inóculo. Portanto, os mesmos modelos que usamos para descrever o acúmulo de inóculo também podem ser usados para descrever o progresso da doença. Iremos seguir a convenção notacional de Vanderplank (1963) e usar x para representar a proporção de plantas infectadas ou a proporção de tecido infectado nas plantas. O uso de uma proporção adimensional com valor entre zero e um para representar a doença torna a matemática muito mais simples do que se usássemos unidades específicas, tal como, por exemplo, a população total de plantas infectadas ou a área total de tecido infectado..
Progresso de doenças monocíclicas
Se o progresso da doença em epidemias monocílicas for linear, o declive da curva de progresso da doença será constante. Além disso, se o progresso da doença numa epidemia monocílica for proporcional à quantidade de inóculo inicial (a qual é uma constante no decurso da epidemia), poderemos tomar o declive da curva de progresso da doença como sendo o produto da quantidade de inóculo inicial com uma constate de proporcionalidade. Portanto, podemos descrever uma epidemia monocílica com progresso linear da doença usando a equação diferencial:
dx/dt = QR
onde dx é um incremento infinitesimal na proporção de doença, dt é um interval de tempo infinitesimal, Q é a quantidade de inóculo inicial, e R é a constante de proporcionlidade que representa a taxa de progresso da doença por unidade de inóculo. Uma vez que Q e R são ambas constantes durante o decurso de uma epidemia, o declive, dx/dt, é constante e o progresso da doença é linear. Tal como com a constante K no modelo de produção monocílica de inóculo, o valor the R representa uma “média” sobre o curso de toda a epidemia. Esse valor depende de múltiplos factores, incluindo a agressividade do patógeno, a susceptibilidade do hospedeiro, as condições ambientais, etc. A unidade de R é proporção por unidade de inóculo inicial por unidade de tempo.
Se integrarmos a equação diferencial acima, obtemos:
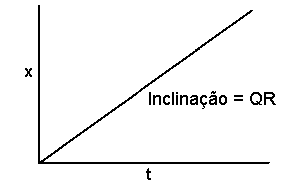
x = QRt
A representação gráfica é uma linha recta com interseção em zero e declive QR
Progresso de doenças policíclicas
Num modelo análogo ao modelo de doenças monocíclicas, a taxa de variação do nível da doença num dado instante é proporcional ao nível da doença no mesmo instante. Portanto, em forma diferencial, a equação que descreve epidemias policíclicas é:
dx/dt = xr
Tal como no modelo monocíclico, x é uma proporção adimensional, com valores entre zero e um, e r é uma constante que depende da média, durante o curso da epidemia, da agressividade do patógeno, da susceptibilidade do hospedeiro, das condições ambientais, etc. Neste caso, o declive dx/dt é proporcional a x, e, portanto, o progresso da doença no tempo occorre de forma acelerada.
Após integração, o modelo toma a forma:
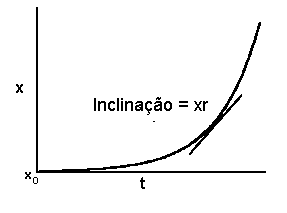
x = x0ert
onde x0 é a proporção (da população ou tecido das plantas) com doença no início da epidemia, e e é a base natural dos logaritmos. Vanderplank (1963) chamou a r “taxa aparente de infecção” porque é baseada no aparecimento de sintomas de doença, os quais têm um atrazo em relação ao início das infecções. A quantidade r é definida como a taxa de aumento de doença por unidade tempo, e tem unidades inversas das do tempo. O parâmetro x0 é por vezes negligentemente chamado de inóculo inicial, com o qual está relacionado; porém, estritamente falando, é o nível inicial da doença (uma proporção). A representação gráfica do modelo tem a familiar forma exponencial:
O limite superior do nível da doença
No modelo acima supõe-se que o nível da doença pode crescer sem limites, o que, é evidente, é impossível; o nível da doença não pode exceder um. Nós podemos ajustar o modelo para corrigir essa deficiência usando o fator (1-x) para representar a proporção de tecido que permanece saudável. Um decréscimo na quantidade de tecido saudável reduz a probabilidade de novas infecções e, portanto, reduz a taxa de progresso da doença.
No limite em que x se aproxima de um, a quantidade de tecido saudável tende para zero, e a taxa de progresso da epidemia decresce até se tornar zero.
O modelo monocíclico de progresso de doença, ajustado ao limite máximo do nível de doença, é:
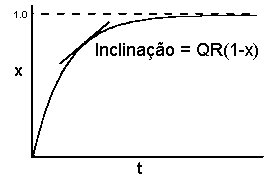
dx/dt = QR(1-x)
Na representação gráfica vemos uma epidemia que no início progride linearmente, mas cujo declive tende para zero à medida que x se aproxima de um.
No modelo policíclico, fazemos um ajuste semelhante:
dx/dt = xr(1-x)
Esse modelo é inicialmente aproximadamente exponencial, mas o seu declive decresce e tende para zero à medida que x aumenta e tende para um. O resultado é uma curva com forma sigmóide:
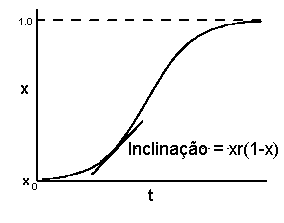
Na realidade, raramente se observa a incidência ou a severidade da doença superando 50% e, quando isso acontece, a forma da curva de progresso da doença não é exactamente sigmóide. Para ler uma discussão sobre outros modelos de progresso de doença, ver Neher & Campbell (1992) e Gilligan (2002).
Estimativa dos parâmetros dos modelos
Transformações
Para aplicar os nossos modelos a epidemias reais, temos que obter valores numéricos para os parâmetros (R no modelo monocíclico, e x0 e r no modelo policíclico). Para estimar os valores desses parâmetros observamos a epidemia, medimos x em diferentes instantes durante a epidemia, e finalmente representamos x em relação a t. A dificuldade está em tentar ajustar modelos não-lineares aos dados. Para este fim, é muito mais fácil transformar x para tentar obter um modelo linear que possa ser ajustado usando regressão linear simples
O modelo monocíclico
No caso do modelo monocíclico, se as observações de x forem transformadas na forma do logaritmo natural de 1/(1-x), e se os valores transformados forem representados em relação a t, obtemos uma linha reta com declive QR.
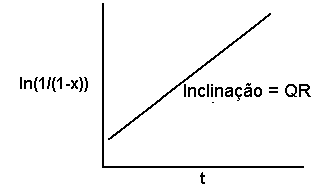
Desde que tenhamos uma estimativa independente do valor de Q, poderemos calcular o valor de R a partir do declive da curva
O modelo policíclico
Se as observações de x num modelo policíclico forem transformadas na forma do logaritmo natural de x/(1-x), e se os valores transformados forem representados em relação a t, obteremos uma linha reta com declive r e interseção igual ao logaritmo natural de x0/(1-x0).
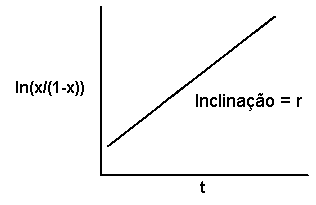
No ajuste de modelos a dados é importante selecionar um modelo baseado no que conhecemos sobre a biologia do patógeno e não só na forma da curva. Do mesmo modo, não devemos tentar fazer inferências sobre a biologia do patógeno com base na forma da curva das observações e no modelo que se ajusta melhor aos dados. Existe variação aleatória em cada observação e, nos modelos transformados, os dados no extremo da linha contribuem de forma não justificada para a determinação do modelo que melhor se ajusta aos dados. É possível que um determinado conjunto de dados seja explicado igualmente bem por modelos que representam diferente biologia, como por exemplo o modelo monocíclico e o modelo policíclico, ou que um conjunto de dados originário de uma epidemia monocíclica seja melhor explicado por um modelo policíclico do que por um modelo monocíclico, e vice-versa.
Alguns exemplos
Exemplo 1, uma epidemia monocíclica: a murcha (fusariose, pt) do linho é causada pelo fungo Fusarium oxysporum f. sp. lini. Clamidosporos do fungo persistem no solo durante vários anos, e quando o linho é plantado num campo infestado, as plantas mais jovens são infectadas através das raízes. Uma pesquisa extensiva do solo foi feita num campo muito infestado, e concluiu-se que este continha em média 57 unidades formadoras de colônias por grama de solo. Quando uma certa variedade suscetível de linho foi plantada neste campo, a percentagem de plantas que mostraram sintomas de doença aumentou no tempo como se segue:
| Dias antes da |
% Plantas |
| Plantação |
Infectadas |
| 10 |
18 |
| 20 |
56 |
| 30 |
82 |
| 40 |
91 |
| 50 |
96 |
| 60 |
98 |
Num gráfico de progresso da doença, nota-se como a percentagem de plantas infectadas se aproxima assintoticamente de 100%.
[Click for larger graph]
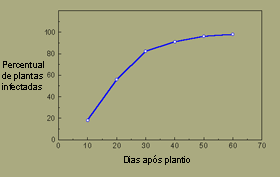
Progresso da murcha (fusariose, pt) do linho
Epidemia monocíclica: murcha do linho
Para estimar o produto, QR, começamos por converter a percentagem de infecção numa proporção, x, e em seguida, usando a transformação aproprida ao modelo monocíclico, calculamos ln(1/(1-x)).
| t |
x |
ln(1/(1-x)) |
| 10 |
.18 |
0.198 |
| 20 |
.56 |
0.821 |
| 30 |
.82 |
1.71 |
| 40 |
.91 |
2.41 |
| 50 |
.96 |
3.22 |
| 60 |
.98 |
3.91 |
A partir de uma representacao de ln(1/(1-x)) em relação a t, ajustamos uma linha reta aos dados usando uma regressão de quadrados mínimos.
[Click for larger graph]
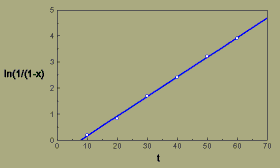
Murcha (fusariose, pt) do linho, transformação multi choque
A estimativa do declive da linha obtido através da regressão, é 0.076, o qual é o valor de QR. Portanto,
R = 0.076/57 = 0.0013/unidade_colonizadora/dia.
Example 2, uma epidemia monocíclica: O crestamento bacteriano aureolado (mancha bacteriana, pt) do feijoeiro é causado pela bactéria Pseudomonas syringae pv. phaseolicola. A principal fonte de inóculo inicial são sementes infectadas, as quais dão origem a plantas com lesões nas folhas primárias. Bactérias produzidas nestas lesões são dispersas através de salpicos de água para plantas saudáveis adjacentes. Novas lesões podem produzir inóculo secundário dentro de 4-5 dias. Em condições moderadamente favoráveis ao desenvolvimento da doença, foram feitas as seguintes observações do seu progresso:
| Dias após o Plantio |
% Plantas
Infectadas |
| 10 |
1 |
| 20 |
4 |
| 30 |
15 |
| 40 |
31 |
| 50 |
65 |
| 60 |
88 |
| 70 |
94 |
O progresso da doença exibe uma curva com forma sigmóide, uma característica das epidemias policíclicas.
[Click for larger graph]
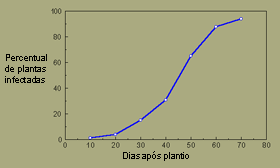
Curva de progresso do crestamento bacteriano aureolado
Tal como na epidemia anterior, convertemos percentagens em proporções (x), mas neste caso usamos a transformação ln(x/(1-x)).
| t
|
x
|
ln(x/(1-x)) |
| 10 |
.01 |
-4.60 |
| 20 |
.04 |
-3.18 |
| 30 |
.15 |
-1.75 |
| 40 |
.31 |
-0.80 |
| 50 |
.65 |
0.62 |
| 60 |
.88 |
1.99 |
| 70 |
.94 |
2.75 |
Representando ln(x/(1-x)), que por vezes é denominado logito de x, em relação a t, podemos ajustar uma linha reta aos dados usando uma regressão de quadrados mínimos
[Clique no gráfico]
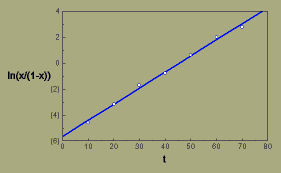
Crestamento bacteriano aureolado (mancha bacteriana, pt) do feijoeiro, transformação logística
A regressão produz um declive de 0.124/dia, o qual é a nossa estimativa da taxa de infecção aparente, r.
Obviamente que, quanto maior for o número de dados que tivermos, e em especial se estes forem distribuídos equilibradamente abaixo e acima de 50% de infecção, tanto melhor será a nossa estimativa da taxa de infecção aparente. No entanto, é possível fazer uma estimativa aproximada da taxa de infecção aparente usando apenas dois dados. Supunhamos que em vez de termos observações com frequência de dez dias durante a epidemia, apenas temos duas observações, uma no estadio inicial (dia 10), e outra no estadio final (dia 70). Como é que poderemos estimar a taxa de infecção aparente?
Neste caso, para calcular o declive usaríamos apenas o primeiro e o último ponto no gráfico dos dados transformados, acima, para calcular o declive::
r = (ln(0.94/(1.0-0.94)) - ln(0.01/1.0-0.01))) / (70 - 10)
= (2.75 + 4.60) / 60
= 0.123/day
Usos práticos dos modelos epidemiológicos
Exemplo 1: Supunhamos que no exemplo da murcha (fusariose, pt) do linho um campo adjacente é investigado, e encontramos um nível de inóculo igual a 1% daquele que temos no nosso campo, o qual exibe definhamento severo. Qual será a incidência de infecção que esperamos encontrar no campo adjacente no fim da estação (60 dias)? Para simplificar os cálculos, supunhamos que a incidência final será baixa, de modo que podemos negligenciar a correcção associada às plantas saudáveis e usar o modelo linear. No nosso exemplo, temos uma média sobre 57 unidades colonizadoras por grama de solo, 1% das quais são 0.57 unidades colonizadoras por grama de solo. Daí calculamos R como sendo 0.0013/unidade_colonizadora/dia, e portanto a proporção de plantas infectadas após 60 dias seria::
x = QRt = (0.57)(0.0013)(60)
= 0.044 ou cerca de 4%
Exemplo 2: Supunhamos que no exemplo do crestamento bacteriano aureolado (mancha bacteriana, pt) do feijoeiro queiramos estimar a incidência máxima de infecção em sementes que pode ser tolerada de modo a que a incidência final da doença não exceda 25%. Iremos supôr que a estação dura 90 dias e, mais uma vez, visto que a incidência final é baixa, iremos negligenciar a correcção logística e usar apenas o modelo exponencial:

Subtituindo x = 0.25, as nossas estimativas de 0.124/dia para r, e de 90 dias para t, obtemos:
0.25 = x0 exp((0.124)(90))
0.25 = x0 exp(11.16)
x0 = 0.25/70263 = 0.0000036
Esta estimativa corresponde a uma incidência máxima de uma infecção em cada 280.000 sementes.
Next: Estratégias de Gestão de Doenças Planta