Si nuestra meta en el manejo de enfermedades de plantas es mantener el desarrollo de enfermedad debajo de un nivel aceptable y comprender el progreso de fitoepidemias en términos cuantitativos, será necesario encontrar algún tipo de modelo matemático para describir la epidemia. Nuestro modelo debería mostrar como alguna variable (preferiblemente algo que podemos contar o medir en el mundo verdadero) cambia con el tiempo. Desde la perspectiva de manejo, observando nuevas infecciones quizás sería los más útil, pero observar estos sucesos microscópicos sería demasiado difícil para ser práctico en la mayoría de los casos. La verificación del inóculo también es muy útil para el manejo de enfermedades y para muchas enfermedades se han desarrollado técnicas prácticas para cuantificar inóculo. Comenzaremos nuestra discusión, por lo tanto, con cambios en el inóculo mediante el tiempo.
Producción monocíclica de inóculo
En epidemias monocíclicas estamos interesados primariamente en el inóculo presente a principios de cada temporada (inóculo inicial). Si usamos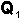 
para representar la cantidad de inóculo inicial a principios de la temporada actual, tendrá el valor de la cantidad de inóculo inicial a principios de la temporada previa, 
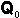, más el incremento que ha resultado del crecimiento del patógeno y desarrollo durante la temporada:
El incremento será una función de la cantidad del inóculo inicial de la temporada previa y un acercamiento razonable es hacerlo una proporción simple de este inóculo,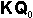 
, donde 
es un constante de proporcionalidad:
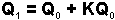
Todos los factores que afectan supervivencia y crecimiento del hongo, producción de propágulos, dispersión de inóculo y muerte del hongo se incorporan en . El valor de . depende de un número grande de factores, incluyendo las condiciones ambientales, el desarrollo del cultivo y las prácticas culturales. Si hay un aumento neto en el inóculo de una temporada a la próxima, será positiva. Por otra parte, si hay una pérdida neta de inóculo, tal como puede ocurrir durante la rotación a un cultivo no hospedero, sería negativa.
A fin de describir los cambios en el inóculo inicial de una temporada a la próxima en un epidemia poliética, generalizaremos el subíndice que indica la temporada.
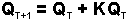
Resolvemos esta ecuación repetidamente, cambiando el subíndice 
indicando tiempo, con cada temporada consecutiva y haciendo el valor actual de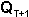 
el valor de 
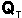en la temporada subsiguiente. A fin de simplificar la ecuación, presumimos un constante (un promedio sobre muchas temporadas). La ecuación arriba mencionada origina el diagrama siguiente:
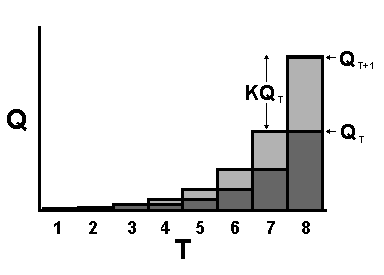
Note que si es positiva, el incremento (el área gris clara sobre cada barra) aumenta con el inóculo inicial en cada temporada consecutiva y el diagrama aparece curvar Polycyclic Inoculum Production
Producción policíclica del inóculo
Para una epidemia policíclica podemos usar esencialmente el mismo modelo en lo que concierne a un patógeno monocíclico inspeccionado durante varias temporadas, donde en vez de repetir el ciclo temporada tras temporada, tenemos muchos ciclos repetidos dentro de la misma temporada. El paso de tiempo cambia a días o semanas en vez de años y debido a que el paso de tiempo no necesariamente es una unidad de tiempo (años), el incremento de tiempo se da como 
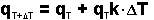
Como una norma de anotación, usaremos la letra minúscula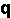 
para representar la cantidad de inóculo durante la epidemia y la minúscula 
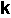para representar la proporción de aumento del inóculo en cada paso. Las unidades de 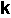corresponden a las unidades de . Por ejemplo, si el tiempo se mide en días, las unidades de 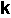sería proporción/día.
La producción de inóculo realmente tiende a ocurrir desigualmente en períodos discretos y descontinuos de infección de duraciones diferentes, dependiendo del tiempo. Por lo tanto, el valor de 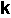probablemente sería diferente para cada período de infección. Sin embargo, según nuestro objetivo de desarrollar el modelo más simple posible que es útil como una herramienta de manejo, simplificaremos el modelo anterior por usar los pasos uniformes de tiempo y suponiendo un constante 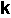(En vez de tener un 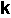que varía según las condiciones ambientales, usaremos un valor de 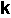"promediada" sobre la epidemia entera.) Primero reestructuramos la ecuación anterior para conseguir:
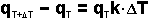
El cambio de la suma del inóculo en un paso de tiempo,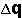 
, es simplemente la diferencia entre la cantidad de inóculo al tiempo y la cantidad de inóculo al tiempo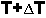 
:
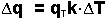
Reestructurando, conseguimos:
Ahora en vez de avanzar el tiempo en pasos discretos, avanzaremos el tiempo continuamente, haciendo infinitesimalmente pequeño:
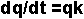
En esta ecuación diferencial,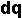 
es un cambio infinitesimalmente pequeño en la cantidad de inóculo y 
es un cambio infinitesimalmente pequeño en el tiempo. Nos dice que el valor de cambio de la cantidad de inóculo es proporcional a la cantidad de inóculo en cualquier punto en el tiempo. Al usar el cálculo, esta ecuación puede integrarse a:
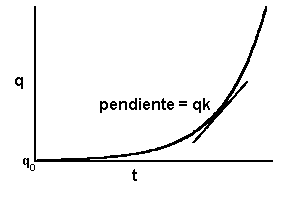
Esto es la función exponencial bien conocida, donde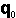 
es el inóculo inicial y 
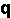es la base del logaritmo natural. El valor instantáneo del cambio en es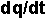 
, la inclinación de la tangente a la curva en cualquier punto.
Continuar: Modelos del Progreso de la Enfermedad
